How To Do Long Division: Your Simple Guide To Solving Big Numbers
Ever wondered how to do long division without feeling completely lost? Well, it's actually a pretty useful skill, even today in 2024. Knowing this method helps you tackle bigger math problems, and that's just a good thing to have in your math toolkit, you know? It's the art of breaking down complex problems into manageable steps, making it an essential tool for students, too.
From my text, we learn that long division is a part of basic arithmetic. It's a method for solving and finding the answer and remainder for division problems that involve numbers with at least two digits, which is really what it's all about. This technique helps you split larger numbers into smaller groups or parts, making the whole thing less scary, you know?
This guide will walk you through how to divide using the long division method, along with some long division examples with answers, so you can see it in action. We'll cover the steps, terms, and give you some good tips. So, whether you're just starting out, or need a quick refresher, this is the article for you if you're looking to learn how to do long division.
- Lia Engel Leaks
- Where Did Steve Horstmeyer Go To High School
- Bhad Bhabie Net Worth
- Jojo Siwa Magazine Cover
- How To Remove Gel Polish
Table of Contents
- What is Long Division?
- Why Learn Long Division?
- The Key Parts of a Division Problem
- Step-by-Step: How to Do Long Division
- Tips for Success with Long Division
- Common Questions About Long Division
- A Quick Recap
What is Long Division?
Long division is a mathematical method for dividing large numbers into smaller groups or parts, that's what my text says. It helps to break down a problem into simple and easy sections, which is pretty handy. This method is different from short division because you show more of your work at each stage to get to the answer, which is often a good thing.
It's a technique for dividing big numbers and even algebraic expressions into many steps following a set order. My text points out it is the most frequently used method for dividing, so it's worth knowing. As we know, division is about sharing a given value or quantity into groups that have equal values, so that's the main idea here.
In long division, values at the individual place, like thousands, hundreds, tens, and ones, are divided one at a time. You always start with the highest place value, which is usually the way to go. This systematic approach makes it possible to handle numbers that would be too much to do in your head, you know, so it's very helpful.
- How To Make An Ender Chest
- Inside Out 2 Always On Phone
- Red Hair Big Boobs
- Valentino Born In Roma
- Cronología De Inter Milan Contra Fc Barcelona
Why Learn Long Division?
In math, few skills are as practical as knowing how to do long division, my text notes. It's really the art of breaking down complex problems into manageable steps, making it a very important tool for students. Knowing this skill helps you build a good foundation for more advanced math concepts, which is pretty cool.
Think about it, long division helps you with things like calculating averages, splitting bills, or even understanding how money is shared among people. It's not just a school thing; it has real-world uses, too. So, learning this method gives you a valuable problem-solving tool that you can use in many different situations, as a matter of fact.
It also helps you get better at mental math and number sense. When you practice long division, you get more comfortable with multiplication and subtraction, which are both parts of the process. This strengthens your overall math skills, which is a big plus, you know? It really does make you feel more capable with numbers.
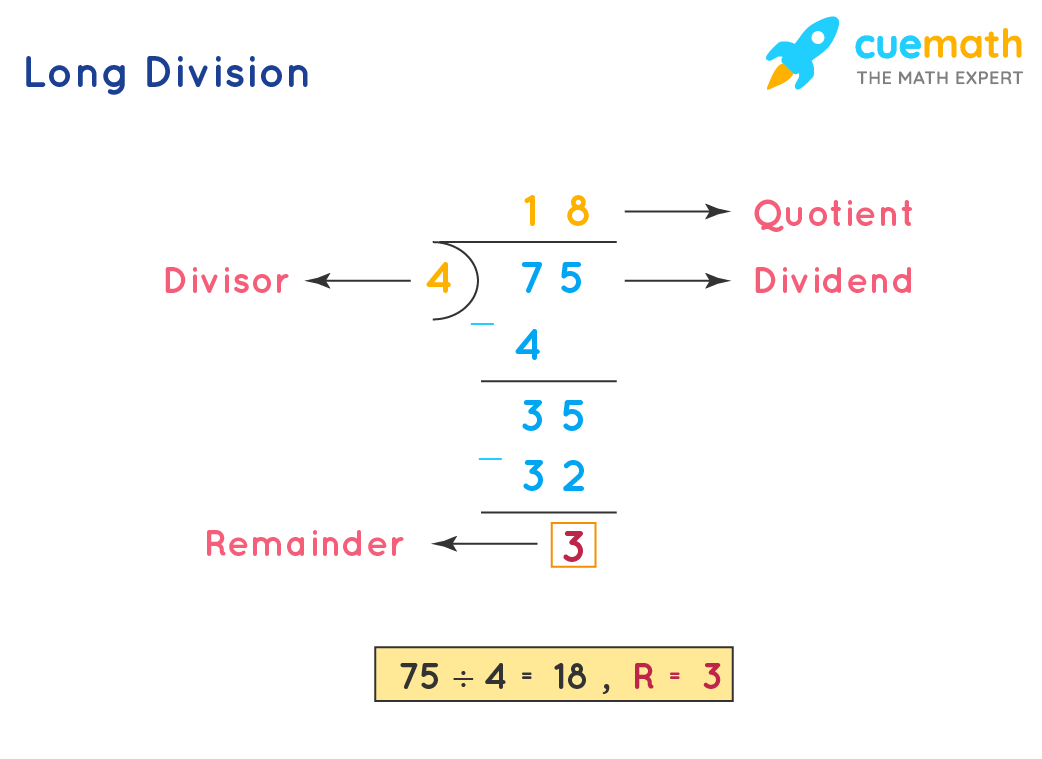
The Key Parts of a Division Problem
Before we jump into the steps, it's good to know the names of the different parts of a division problem. This makes it easier to follow along and understand what's happening. So, we have a few main terms, which are important.
- Dividend: This is the big number that you are dividing. It's the total amount you want to split up.
- Divisor: This is the number you are dividing by. It tells you how many groups you want to make, or how many are in each group.
- Quotient: This is your answer! It's the result of the division, showing how many times the divisor fits into the dividend.
- Remainder: Sometimes, the divisor doesn't fit perfectly into the dividend. The number left over at the end is called the remainder. It's what couldn't be evenly divided, you know?
For example, in 10 ÷ 3 = 3 with a remainder of 1: 10 is the dividend, 3 is the divisor, 3 is the quotient, and 1 is the remainder. Understanding these terms makes the whole process a lot clearer, which is good.
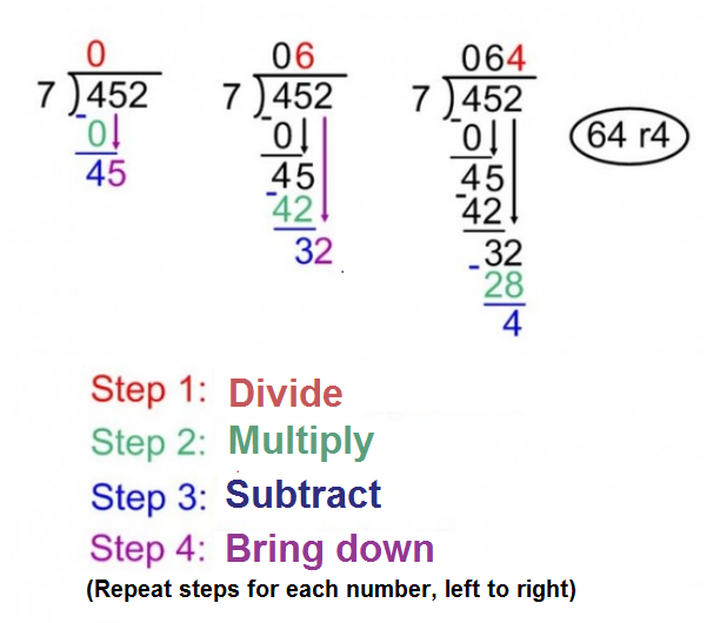
Step-by-Step: How to Do Long Division
Let's get into the actual process. We'll use a common way of writing out long division, which you'll see often. It's a sequence of steps you repeat until you have your answer. So, here are the main steps, which are pretty much always the same.
- Divide: See how many times the divisor goes into the first part of the dividend.
- Multiply: Multiply the quotient digit you just found by the divisor.
- Subtract: Take that product away from the part of the dividend you were working with.
- Bring Down: Bring down the next digit from the dividend to form a new number.
- Repeat: Do steps 1-4 again until there are no more digits to bring down.
People often remember these steps with a little phrase like "Does McDonald's Sell Burgers Regularly?" or "Dad, Mom, Sister, Brother, Rover," with each word starting with the letter of a step. This helps you keep track, which is a neat trick.
Example 1: No Remainder
Let's try dividing 735 by 5. This is a pretty straightforward one to start with, you know.
Problem: 735 ÷ 5
Step 1: Set up the problem.
You write the divisor (5) outside the division symbol and the dividend (735) inside. It looks a bit like a house, so that's how some people remember it.
Step 2: Divide the first digit.
Look at the first digit of the dividend, which is 7. How many times does 5 go into 7? It goes in 1 time. Write this 1 above the 7 in the quotient spot, so that's your first number in the answer.
Step 3: Multiply.
Now, multiply that 1 by your divisor, 5. So, 1 × 5 = 5. Write this 5 directly below the 7, which is pretty important for the next step.
Step 4: Subtract.
Subtract the 5 from the 7. So, 7 - 5 = 2. Write this 2 below the 5. This is the remainder for just this part of the problem, you know.
Step 5: Bring Down.
Bring down the next digit from the dividend, which is 3. Place it next to the 2 you just got. Now you have 23. This new number is what you'll work with next, as a matter of fact.
Step 6: Repeat the process (Divide again).
How many times does 5 go into 23? It goes in 4 times, because 5 × 4 = 20. Write this 4 next to the 1 in the quotient spot, above the 3. So, your quotient is starting to take shape.
Step 7: Multiply again.
Multiply the new quotient digit, 4, by the divisor, 5. So, 4 × 5 = 20. Write this 20 directly below the 23. This is just how the steps go, you know.
Step 8: Subtract again.
Subtract 20 from 23. So, 23 - 20 = 3. Write this 3 below the 20. This is your new little remainder for this part, which is pretty common.
Step 9: Bring Down again.
Bring down the last digit from the dividend, which is 5. Place it next to the 3 you just got. Now you have 35. This is your final number to divide, so we're almost done.
Step 10: Repeat one last time (Divide).
How many times does 5 go into 35? It goes in 7 times, because 5 × 7 = 35. Write this 7 next to the 4 in the quotient spot, above the 5. Your quotient is now 147, which is pretty much the answer.
Step 11: Multiply and Subtract one last time.
Multiply 7 by 5, which is 35. Subtract 35 from 35, and you get 0. Since there are no more digits to bring down and your remainder is 0, you are finished. So, the answer is 147, you know.
Answer: 735 ÷ 5 = 147
Example 2: With a Remainder
Now, let's try one where things don't divide perfectly. We'll divide 458 by 7. This shows you how to handle that leftover part, which is called a remainder.
Problem: 458 ÷ 7
Step 1: Set up the problem.
Write the divisor (7) outside and the dividend (458) inside the division symbol. This is just like before, so it's a familiar start.
Step 2: Divide the first part.
Look at the first digit of the dividend, 4. Can 7 go into 4? No, it can't. So, you take the first two digits, which are 45. How many times does 7 go into 45? It goes in 6 times, because 7 × 6 = 42. Write this 6 above the 5 in the quotient spot, you know.
Step 3: Multiply.
Multiply the 6 by the divisor, 7. So, 6 × 7 = 42. Write this 42 directly below the 45. This keeps everything organized, which is good.
Step 4: Subtract.
Subtract 42 from 45. So, 45 - 42 = 3. Write this 3 below the 42. This is the amount left over from this section, as a matter of fact.
Step 5: Bring Down.
Bring down the next digit from the dividend, which is 8. Place it next to the 3 you just got. Now you have 38. This is the new number you need to work with, which is pretty typical.
Step 6: Repeat the process (Divide again).
How many times does 7 go into 38? It goes in 5 times, because 7 × 5 = 35. Write this 5 next to the 6 in the quotient spot, above the 8. So, your quotient is building up, you know.
Step 7: Multiply again.
Multiply the new quotient digit, 5, by the divisor, 7. So, 5 × 7 = 35. Write this 35 directly below the 38. You're just following the steps here, which is pretty easy once you get the hang of it.
Step 8: Subtract again.
Subtract 35 from 38. So, 38 - 35 = 3. Write this 3 below the 35. This is your final leftover number, so that's your remainder.
Step 9: Check for more digits.
Are there any more digits to bring down from the dividend? No, there aren't. So, you're done with the division. The number 3 is your remainder, which is just what's left over.
Answer: 458 ÷ 7 = 65 with a remainder of 3. You can write this as 65 R 3. So, that's how you deal with those numbers that don't divide evenly.
Tips for Success with Long Division
Learning how to do long division can feel like a lot at first, but with a few good tips, you'll get much better at it. These little tricks can make a big difference, you know.
- Know Your Multiplication Tables: This is probably the most important thing. If you know your times tables well, the "divide" and "multiply" steps will be much faster and easier. Practice them often, which is a good idea.
- Practice, Practice, Practice: Just like anything new, the more you do it, the better you become. Start with easier problems and slowly work your way up to more difficult ones. So, that's really key.
- Keep Your Work Neat: Line up your numbers carefully. If your digits are messy or out of line, it's very easy to make a mistake, especially during subtraction or when bringing numbers down. Use graph paper if it helps, as a matter of fact.
- Estimate First: Before you even start, try to guess what the answer might be. For example, for 735 ÷ 5, you know 700 ÷ 5 is 140, so your answer should be around that. This helps you catch big mistakes, you know?
- Check Your Work: Once you have your answer, you can check it. Multiply your quotient by your divisor, then add any remainder. This should give you your original dividend. For example, 147 × 5 = 735. For the other one, (65 × 7) + 3 = 455 + 3 = 458. So, that's a good way to be sure.
- Don't Rush: Take your time with each step. There's no need to speed through it. Focusing on accuracy is much better than trying to be fast, you know.
Common Questions About Long Division
People often have similar questions when they are learning how to do long division. Let's try to answer a few of those, which is pretty helpful.
What are the steps to long division?
The steps are: Divide, Multiply, Subtract, Bring Down, and then Repeat. This sequence of actions is what you do over and over until you have your answer and any remainder. It's a cycle, so you just keep going through it, you know.
What is the easiest way to do long division?
The easiest way is to know your multiplication facts really well and to keep your work very neat. Breaking the problem down into those five small steps makes it much more manageable than trying to see the whole answer at once. So, practice those steps and keep things tidy, as a matter of fact.
How do you check your long division answer?
To check your answer, you just multiply your quotient by your divisor. If there's a remainder, you add that to the product. The final number should be the same as your original dividend. This is a good way to confirm you got it right, you know?
A Quick Recap
Learning how to do long division is a really good skill to have. It helps you break down big numbers into smaller, more manageable parts, which is super useful. We've gone through the steps: Divide, Multiply, Subtract, Bring Down, and Repeat, which are the heart of the method.
Remembering the terms like dividend, divisor, quotient, and remainder will make things clearer as you work through problems. And don't forget those tips, like knowing your multiplication tables and keeping your work neat. With a bit of practice, you'll be solving these problems with more confidence, you know?
If you want to learn more about division on our site, there's plenty to explore. Also, feel free to check out our other math guides for more help. For more math practice and explanations, you can also visit Math Is Fun, which is a good resource.
- What Is A Sapiosexual
- Dr Pepper Creamy Coconut
- Bbq Chicken Urban Dictionary
- Meaning Of Am Pm In Time
- Four Seasons Orlando Baby

Long Division Video – Corbettmaths Primary
Long Division | How to do Long Division | Examples | Solutions
Long Division Steps By Step