How To Turn Decimals Into Fractions: Your Friendly Step-by-Step Guide

Maia Kirlin 25 Aug 2025

Ever looked at a decimal number and wished you could just, you know, turn it into a fraction? Maybe you're helping with homework, or perhaps you're just brushing up on some math skills. Well, the good news is that converting decimals to fractions is a really useful skill, and it's actually not as tricky as it might seem at first glance. It's a fundamental part of understanding how numbers work, and it helps you see the same value in a slightly different way, which is pretty neat.

This skill, in a way, helps you grasp the true essence of numbers, allowing you to express parts of a whole in a form that might feel more tangible. From "My text," we learn that converting a decimal to a fraction is the process of changing a number in decimal form into a fraction, which represents the same value in terms of parts of a whole number. It's about seeing how those decimal places truly relate to something like a slice of pie or a portion of a larger quantity, which is, you know, quite practical.

So, whether you're dealing with a straightforward decimal or one that keeps on going, this guide will walk you through the process. We'll explore how to handle different kinds of decimals, from those that stop neatly to the ones that repeat, and we'll even touch upon how to simplify your answers. You'll find out how to deal with whole numbers, recurring decimals, and different powers of 10, basically getting you set up for success, which is, you know, what we want.

Understanding the Basics: What Are Decimals and Fractions?
The Simple Way: Converting Terminating Decimals
Tackling Tricky Repeating Decimals
- One Repeating Digit
- Multiple Repeating Digits
Why Simplify Your Fractions?
Quick Tips for Success
Frequently Asked Questions About Decimal to Fraction Conversion
Your Next Steps in Number Conversion

Understanding the Basics: What Are Decimals and Fractions?

Before we jump into converting, it's pretty helpful to get a quick refresher on what decimals and fractions actually are. Decimals, you know, are a way of showing numbers that aren't whole, using a decimal point to separate the whole part from the fractional part. For instance, 0.5 means half of something, and 3.25 means three whole things and a quarter of another. The decimal numeral system is a positional numeral system, which means the position of each digit tells you its value, which is, like, really important.

Fractions, on the other hand, show parts of a whole by using a top number (the numerator) over a bottom number (the denominator). The denominator tells you how many equal parts the whole is divided into, and the numerator tells you how many of those parts you have. So, 1/2 is one part out of two, and 3/4 is three parts out of four. Both decimals and fractions are just different ways of writing the same value, in a way, which is pretty cool when you think about it.

The Simple Way: Converting Terminating Decimals

Terminating decimals are the easiest kind to work with because, well, they stop. They don't go on forever. Think of numbers like 0.75 or 0.2. From "My text," we learn that converting decimals into fractions isn't hard, and for these, it's a straightforward three-step process, which is, you know, quite manageable.

Step 1: Figure Out the Place Value

The first thing you want to do is look at the last digit of your decimal and see what its place value is. This is, you know, pretty crucial. For example:

In 0.7, the 7 is in the tenths place.
In 0.75, the 5 is in the hundredths place.
In 0.125, the 5 is in the thousandths place.

Basically, you count how many digits are after the decimal point. That number tells you which power of 10 you're dealing with. One digit means tenths (10^1), two digits mean hundredths (10^2), three digits mean thousandths (10^3), and so on. This step is, like, really the foundation.

Step 2: Write It as a Fraction

Now, you take the digits after the decimal point and make them the top number (numerator) of your fraction. The bottom number (denominator) will be the place value you found in Step 1. So, if it was tenths, your denominator is 10; if it was hundredths, it's 100, and so on. "To write a decimal as a fraction in simplest form, write the decimal digits above," says "My text," which is, you know, a very clear instruction.

0.7 becomes 7/10 (because 7 is in the tenths place).
0.75 becomes 75/100 (because 75 goes out to the hundredths place).
0.125 becomes 125/1000 (because 125 goes out to the thousandths place).

This is, in some respects, the easiest part once you get the hang of place values.

Step 3: Make It Simple

Most of the time, the fraction you get in Step 2 won't be in its simplest form. This means you can divide both the top and bottom numbers by the same number (a common factor) until you can't anymore. This is often called finding the Greatest Common Factor (GCF). "Before you learn how to do this, you should also know how to simplify," "My text" reminds us, which is, you know, good advice.

For 7/10: There's no common factor other than 1, so it's already simple.
For 75/100: Both can be divided by 25. 75 ÷ 25 = 3, and 100 ÷ 25 = 4. So, 75/100 simplifies to 3/4.
For 125/1000: Both can be divided by 125. 125 ÷ 125 = 1, and 1000 ÷ 125 = 8. So, 125/1000 simplifies to 1/8.

Simplifying is, actually, a really important step because it gives you the most precise and easy-to-use version of the fraction. You know, it's like tidying up your answer.

Handling Whole Numbers with Decimals

What if you have a number like 3.25? This is, you know, a mixed number. The whole number part (3) just stays as a whole number. You convert the decimal part (0.25) into a fraction, just like we did above. So, 0.25 becomes 25/100, which simplifies to 1/4. Then, you put the whole number back with the fraction, making it 3 and 1/4. This is, basically, how you get a mixed number as the answer, which "My text" mentions as a possibility.

Tackling Tricky Repeating Decimals

Repeating decimals are a bit more involved, but still totally doable. These are decimals where one or more digits keep repeating forever, like 0.333... (which is 0.3 with a bar over the 3) or 0.121212... (which is 0.12 with a bar over the 12). "Learn how to convert terminating and repeating decimals to fractions using three simple steps," "My text" says, and that's, you know, what we'll do here.

One Repeating Digit

Let's take 0.333... (or 0.3 with a bar). Here’s how you approach it, basically:

Let 'x' equal the decimal: x = 0.333...
Multiply 'x' by 10 (because one digit repeats): 10x = 3.333...
Subtract the first equation from the second: 10x = 3.333... - x = 0.333... ----------------- 9x = 3
Solve for 'x': x = 3/9.
Simplify: x = 1/3.

So, 0.333... is, you know, really 1/3. This method is, actually, quite clever for capturing that infinite repetition.

Multiple Repeating Digits

What if you have something like 0.121212...? The process is quite similar, just a little different with the multiplication:

Let 'x' equal the decimal: x = 0.121212...
Multiply 'x' by 100 (because two digits repeat): 100x = 12.121212...
Subtract the first equation from the second: 100x = 12.121212... - x = 0.121212... --------------------- 99x = 12
Solve for 'x': x = 12/99.
Simplify: Both 12 and 99 can be divided by 3. 12 ÷ 3 = 4, and 99 ÷ 3 = 33. So, x = 4/33.

You know, the key here is to multiply by a power of 10 that shifts the repeating part so it lines up perfectly for subtraction. This allows you to, basically, eliminate the endless decimal, which is pretty neat.

Why Simplify Your Fractions?

Simplifying fractions is, you know, more than just making them look nicer. It makes them easier to work with in future calculations, and it's the standard way to present a fractional answer. A fraction like 50/100 is technically correct for 0.5, but 1/2 is much clearer and more concise. It's like saying "half" instead of "fifty out of one hundred," which is, you know, just more direct. "Instantly convert decimals into fractions and reduce the results to simplest form with this free" tool, "My text" mentions, highlighting the importance of this final step.

Always aim for the simplest form. If you're ever unsure, you can, like, keep dividing by small prime numbers (2, 3, 5, 7, etc.) until you can't divide both the numerator and denominator by the same number anymore. This ensures you've reached the absolute simplest version, which is, you know, the goal.

Quick Tips for Success

Use Place Values: Really understand tenths, hundredths, thousandths. This is the foundation for terminating decimals, you know.
Practice Simplification: The more you simplify fractions, the quicker and easier it becomes. It's, like, a muscle you train.
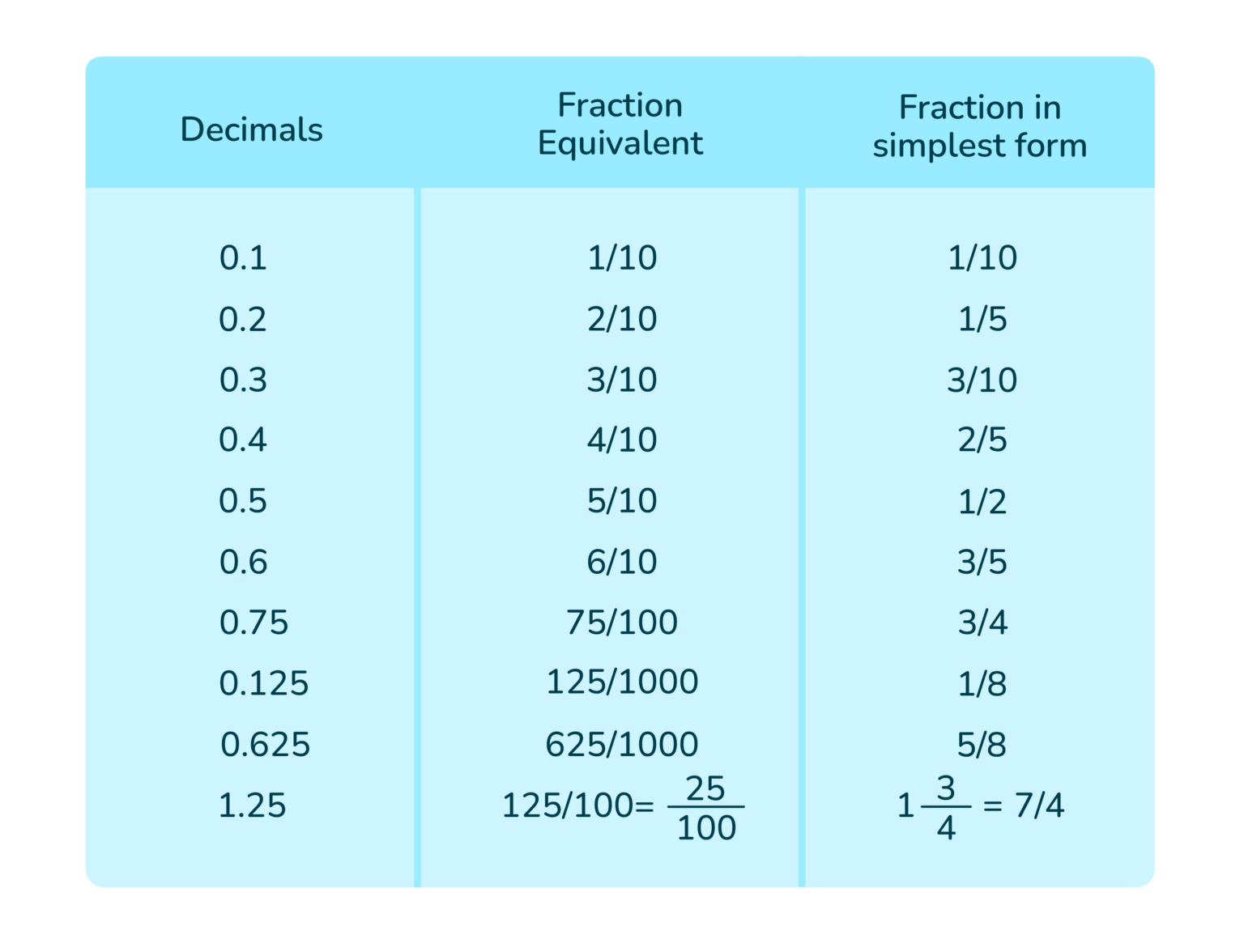
Recognize Common Conversions: Over time, you'll start to recognize common decimal-fraction pairs, like 0.5 = 1/2, 0.25 = 1/4, 0.75 = 3/4, 0.2 = 1/5, and 0.333... = 1/3. "My text" suggests seeing a handy chart with common decimal/fraction conversions, which is, you know, super helpful.
Don't Fear Calculators (But Understand the Process): While a decimal to fraction calculator is a digital tool that performs this conversion instantly, providing, you know, quick answers, it's still important to grasp the manual steps. Understanding the "how" is, actually, more valuable than just getting the answer. You can learn how to use simple or advanced calculators to convert decimals into fractions with ease, according to "My text," but, you know, knowing the steps yourself is key.
Be Patient: If it doesn't click right away, that's okay. Math often takes a little time and practice. Just keep at it, and you'll get there, you know, eventually.

Frequently Asked Questions About Decimal to Fraction Conversion

Here are some questions people often ask about turning decimals into fractions, which are, you know, pretty common concerns:

How do you convert a decimal to a fraction without a calculator?

You convert a decimal to a fraction without a calculator by using place values. For terminating decimals, you write the decimal digits as the numerator and the corresponding power of 10 (like 10, 100, 1000) as the denominator. Then, you simplify the fraction. For repeating decimals, you set the decimal equal to 'x', multiply by a power of 10 to shift the repeating part, subtract the original equation, and then solve for 'x'. This is, you know, the manual method we just went over.

What are the three steps to convert a decimal to a fraction?

The three main steps to convert a terminating decimal to a fraction are: 1. Determine the place value of the last digit in the decimal. 2. Write the decimal digits as the numerator and the place value as the denominator. 3. Simplify the resulting fraction to its lowest terms. For repeating decimals, the steps are a bit different, as we discussed, involving algebraic manipulation, which is, you know, a different kind of process.

Can all decimals be written as fractions?

Yes, in a way, all rational decimals can be written as fractions. This includes both terminating decimals (like 0.5, which is 1/2) and repeating decimals (like 0.333..., which is 1/3). However, there are also irrational numbers, like pi (π) or the square root of 2, which have decimal representations that go on forever without repeating. These, you know, cannot be written as simple fractions, which is a key distinction.

Your Next Steps in Number Conversion

Learning how to turn decimals into fractions is, you know, a really important math skill. It helps you understand numbers better and makes it easier to work with them in different situations. From "My text," we know that converting decimals into fractions is a key skill, and it's something that comes up in many areas, from everyday life to more advanced math. With the steps we've covered today, you're pretty much ready to tackle most decimal-to-fraction conversions.

So, why not try a few on your own? Pick some decimals, maybe some terminating ones, and then some repeating ones, and see if you can convert them and simplify the fractions. You can always check your work with an online converter if you need to, but the real learning comes from doing it yourself. Learn more about fractions and decimals on our site, and you can find more practice problems on this page, which is, you know, a good next step. Keep practicing, and you'll be a pro in no time, basically!

Fraction-decimal Chart in Illustrator, PDF - Download | Template.net

How to Convert Fractions to Decimals: 14 Steps (with Pictures)

How to Convert Decimals to Fractions - DoodleLearning

Pigimail Entertainment