Unlocking The Area Of A Pentagon: Your Guide To Calculating This Unique Shape

Kennedi Carroll Jr. 25 Aug 2025

Have you ever looked at a pentagon and wondered how to figure out its size? It's a shape that, you know, really pops up in some interesting places, from famous buildings to cool designs. Figuring out the space it covers, its area, can seem a bit tricky at first, but honestly, it's pretty straightforward once you get the hang of it. We're going to walk through exactly how to do that, making sure you feel confident with the numbers.

A pentagon, for those who might be wondering, is essentially a polygon with five straight sides and five angles. When all its sides are the same length and all its angles are equal, we call it a "regular pentagon." These regular ones are the kind you typically see in math problems and, well, they're usually what people think of when they hear the word "pentagon." Understanding how to find its area is a rather useful skill, whether you're a student, a designer, or just someone curious about the world around you, as a matter of fact.

So, this article is here to break down the ways you can calculate the area of a pentagon. We'll look at different formulas, depending on what information you already have, and we'll even work through some real examples. We'll talk about everything from using the side length to something called an apothem, and even how a radius plays into it. By the time we're done, you'll have a much clearer picture, definitely, of how these calculations come together.

What Exactly is a Pentagon, Anyway?
Why Does Calculating a Pentagon's Area Matter?
The Core Formula: Area of a Regular Pentagon with Side Length (s)
Using Apothem and Perimeter: A Handy Alternative
When You Only Have the Radius: From Center to Vertex (r)
Dealing with Irregular Pentagons: A Different Approach
- Breaking It Down into Triangles
- The Coordinate Method
Practical Tips for Accuracy and Rounding
- Rounding to Two Decimal Places
- Using Calculators and Tools
Common Questions About Pentagon Area
Putting It All Together: Why This Matters

What Exactly is a Pentagon, Anyway?

A pentagon, at its core, is a geometric shape with five straight sides and five angles. You know, it's pretty simple in that regard. When we talk about a "regular pentagon," we mean that all five of its sides are the same length, and all five of its internal angles are equal, each measuring 108 degrees. This kind of symmetry makes calculating its area much more predictable, honestly.

On the other hand, there are "irregular pentagons," where the sides and angles can be all sorts of different sizes. These are a bit more challenging to work with, but still possible to figure out. For most of our discussion today, we'll be focusing on the regular kind, as that's what typically comes up when people ask about the area of a pentagon, you know.

Why Does Calculating a Pentagon's Area Matter?

You might think, "When am I ever going to need this?" But actually, pentagons pop up more than you'd expect in the real world. Think about architecture, for instance. The most famous example, of course, is The Pentagon building, which is literally the largest office building in the world in terms of its ground area. Knowing how to calculate its space is kind of essential there, right?

Beyond massive buildings, pentagons appear in design, art, and even nature. Many star shapes are formed from pentagons, and some flowers or fruits show pentagonal symmetry. So, whether you're designing a unique floor plan, creating a complex graphic, or just trying to understand the geometry around you, knowing how to find the area of a pentagon is a pretty neat skill to have, to be honest.

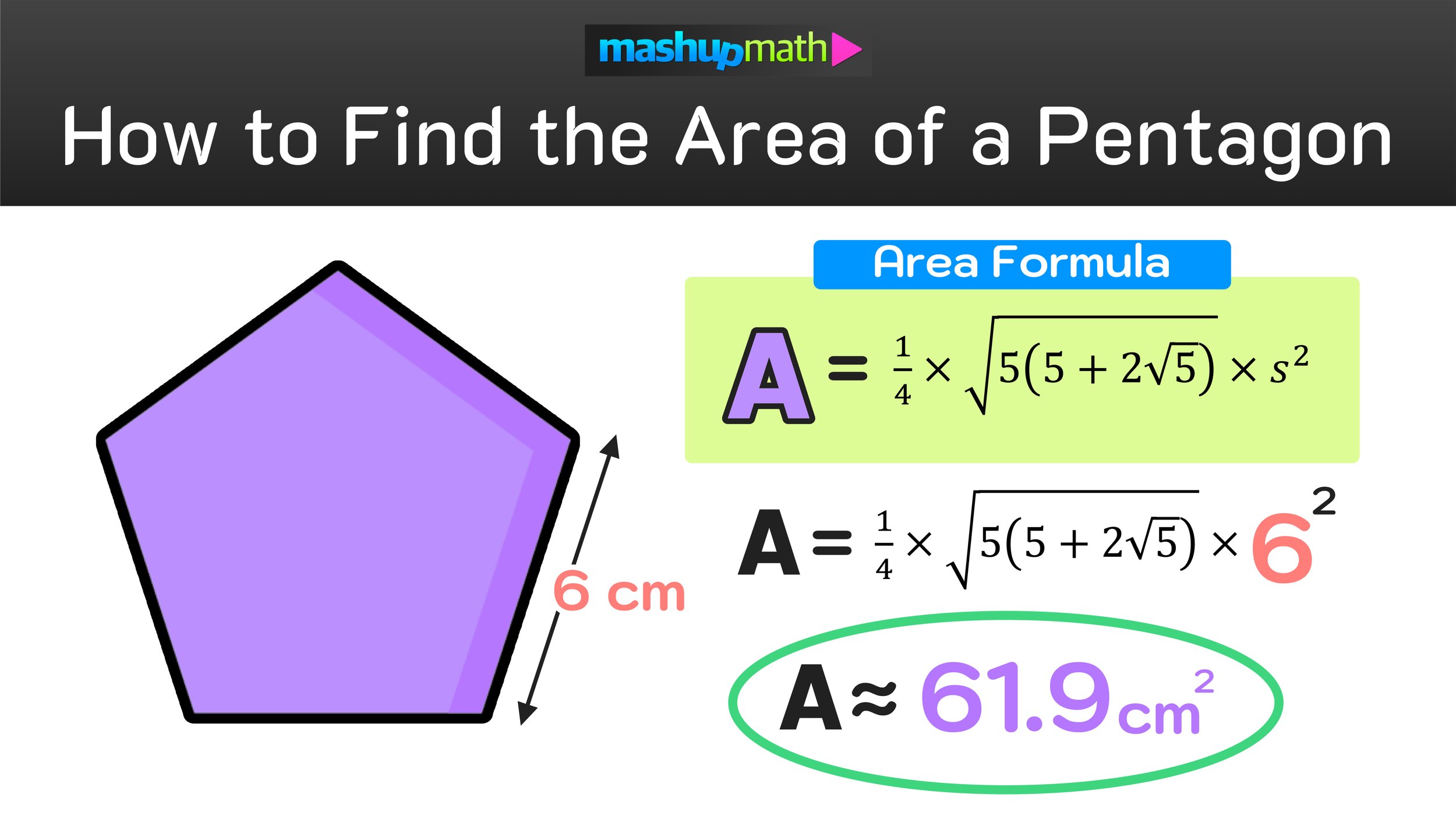
The Core Formula: Area of a Regular Pentagon with Side Length (s)

When you have a regular pentagon and you know the length of one of its sides (which we'll call 's'), there's a really handy formula you can use. This is, you know, one of the most common ways to find the area. It’s a direct method, and it works wonderfully if you have that side measurement ready.

Explaining the Formula: Area = (5 × s²) / (4 × tan(π/5))

The formula for the area of a regular pentagon, as seen in my text, is: Area = (5 × s²) / (4 × tan(π/5)). Let's break that down a little. Here, 's' stands for the length of one side of the pentagon. The 'π' (pi) is that mathematical constant, approximately 3.14159, and 'tan' is the tangent function you'd find on your calculator. The 'π/5' part is essentially the angle in radians that corresponds to the central angle of one of the five triangles that make up the pentagon, you know, when you slice it from the center. It's basically 36 degrees, if you're thinking in degrees.

This formula, you know, essentially comes from dividing the pentagon into five identical triangles, all meeting at the center. Then, it uses trigonometry to find the area of one of those triangles and multiplies it by five. It's a rather elegant way to get to the total area, actually, and it's super reliable.

Step-by-Step Guide for Side Length

To use this formula, here’s what you do, step by step:

**Find the side length (s):** Make sure you have this measurement for your regular pentagon.
**Calculate s²:** Just multiply the side length by itself.
**Compute tan(π/5):** Use your calculator for this. Make sure your calculator is set to radians, or if you prefer degrees, you'd calculate tan(36°).
**Multiply 5 by s²:** This gives you the top part of the fraction.
**Multiply 4 by tan(π/5):** This gives you the bottom part of the fraction.
**Divide the top by the bottom:** Your result is the area of the pentagon.

And then, you know, always remember to include the correct units, like cm² or m², for your final answer. It really makes a difference for clarity.

Example: Calculating with a Given Side

Let's say we have a regular pentagon where each side (s) measures 7 cm. We want to find its area. So, we'd follow our steps:

**s = 7 cm**
**s² = 7 cm × 7 cm = 49 cm²**
**tan(π/5)** (or tan(36°)) is approximately **0.72654**
**5 × s² = 5 × 49 = 245**
**4 × tan(π/5) = 4 × 0.72654 = 2.90616**
**Area = 245 / 2.90616 ≈ 84.309 cm²**

Rounding to two digits after the decimal point, as my text suggests, the area would be approximately **84.31 cm²**. Pretty straightforward, you know, once you have the numbers in place.

Using Apothem and Perimeter: A Handy Alternative

Sometimes, you might not have the side length directly, but you might know the apothem and the perimeter. This is another very common and useful way to figure out the area, especially for regular polygons. It's actually a bit more general, applying to any regular polygon, not just pentagons, which is kind of cool.

What is an Apothem?

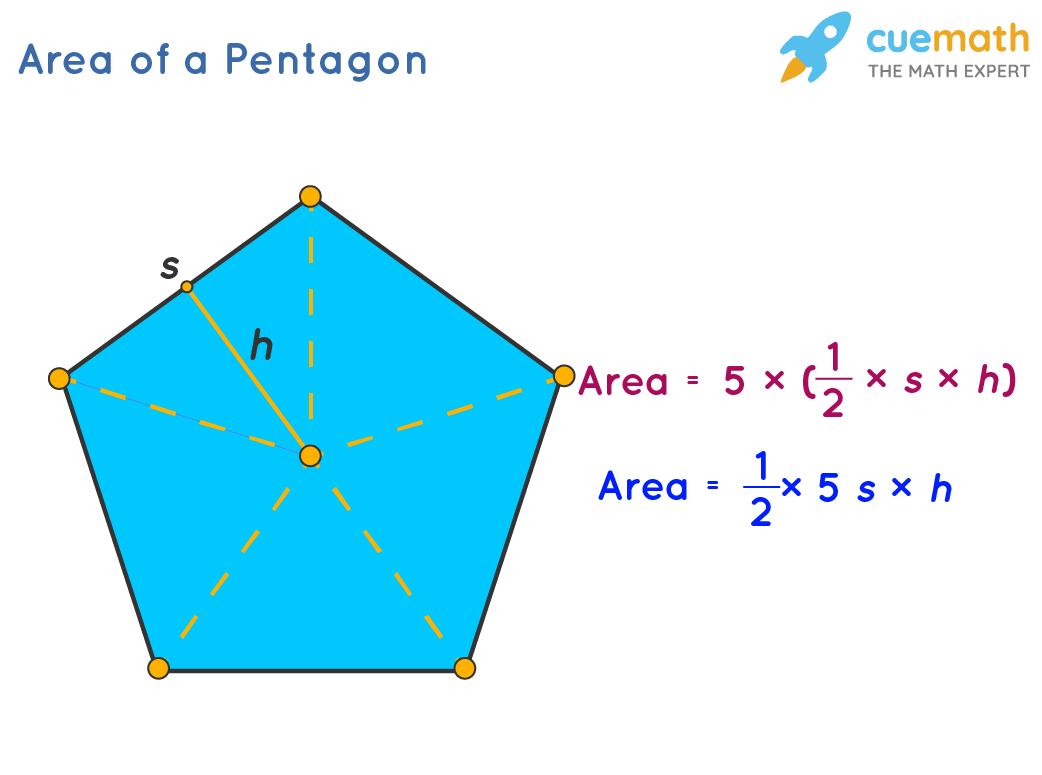
The apothem of a regular polygon is essentially the distance from the very center of the polygon to the midpoint of one of its sides. It always forms a right angle with that side. Think of it as the shortest distance from the center to any side. It's a pretty important measurement, really, when you're working with these shapes.

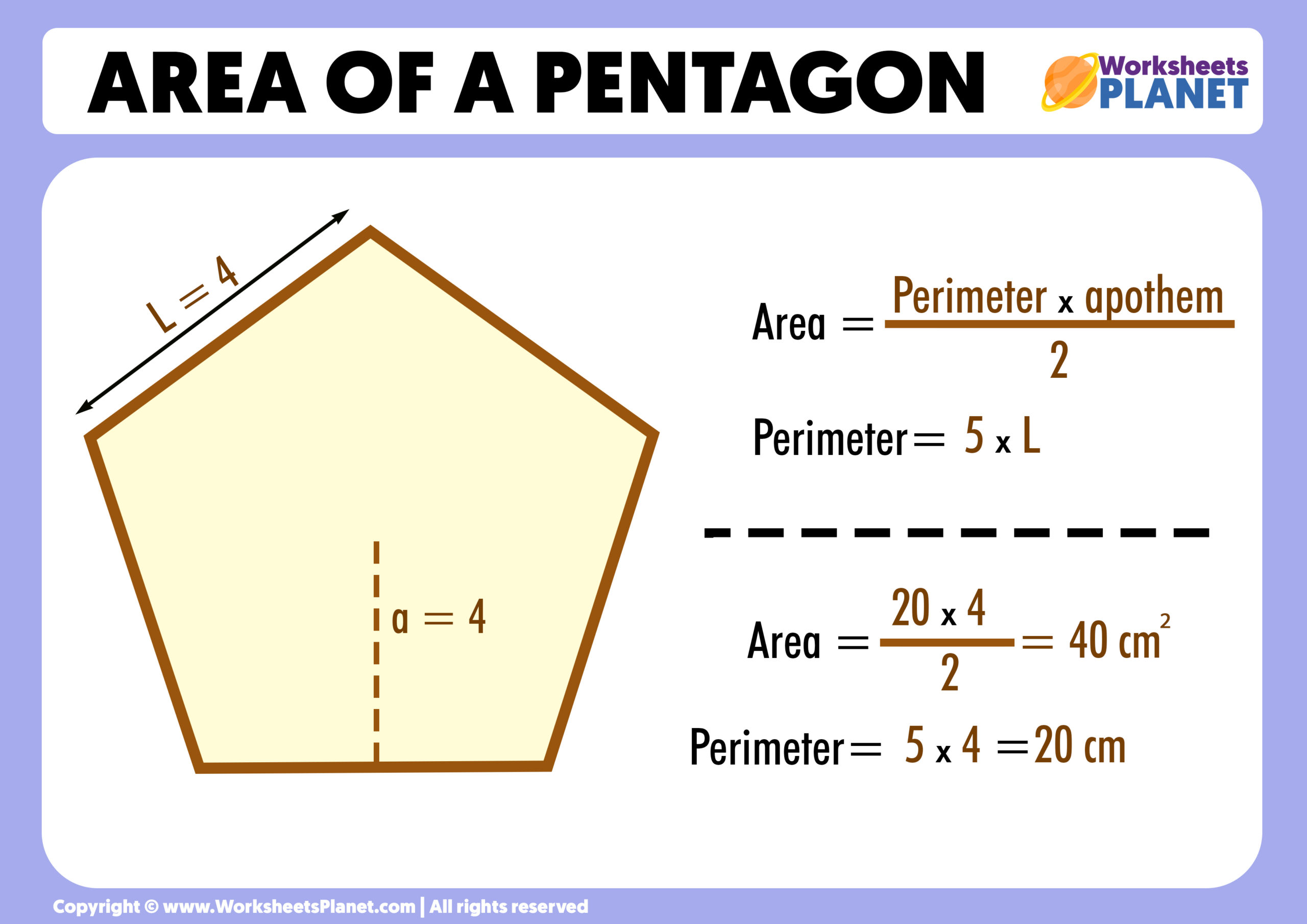
The Formula: Area = (1/2) × apothem × perimeter

The formula for the area of any regular polygon, including a pentagon, is Area = (1/2) × apothem × perimeter. This makes a lot of sense if you think about it. Imagine unfolding the pentagon into five triangles; the apothem is the height of each triangle, and the perimeter is the sum of all their bases. This formula, you know, pretty much just adds up the areas of those triangles in one go.

Example from My Text: Apothem 3 cm, Perimeter 21.8 cm

My text provides a great example: "A regular pentagon has an apothem measuring 3 cm and a perimeter of 21.8 cm." Let's find its area using this information.

**Apothem (a) = 3 cm**
**Perimeter (P) = 21.8 cm**

Now, we just plug these numbers into our formula:

**Area = (1/2) × a × P**
**Area = (1/2) × 3 cm × 21.8 cm**
**Area = 1.5 cm × 21.8 cm**
**Area = 32.7 cm²**

This result is already rounded to one decimal place, but if we needed to round to two digits after the decimal point, it would be **32.70 cm²**. That's a rather quick way to get the answer when you have these specific measurements, you know.

When You Only Have the Radius: From Center to Vertex (r)

What if you only know the distance from the center of the pentagon to one of its corners? This measurement is called the radius (r). My text mentions scenarios like "A regular pentagon is inscribed in a circle whose radius measures 9 inches." In such cases, you can still find the area, but you'll need an extra step, basically, to figure out the side length first.

Understanding the Radius

For a regular pentagon, the radius is the distance from its center to any of its vertices (corners). If you imagine drawing a circle that touches all the vertices of the pentagon, the radius of that circle is exactly what we're talking about here. It's a key measurement, you know, for understanding the overall size of the shape.

How to Find the Side (s) from Radius: s = 2r sin(π/5)

My text tells us that "The side can be computed using the formula s = 2r sin(π/5), where r is the length from the center of a pentagon to a vertex." This formula is super useful. Here, 'r' is your radius, and 'sin' is the sine function, again, usually found on your calculator. Just like before, 'π/5' refers to that 36-degree angle. This calculation helps you bridge the gap between knowing the radius and getting the side length, which you then need for the area formula.

Then, Back to the Side Length Formula

Once you've calculated the side length 's' using the radius formula, you're pretty much back to square one with the first method we discussed. You take that newly found 's' value and plug it into the main area formula: Area = (5 × s²) / (4 × tan(π/5)). So, it's kind of a two-step process, but still very doable, you know.

Example from My Text: Radius 9 Inches

Let's use the example from my text: "A regular pentagon is inscribed in a circle whose radius measures 9 inches."

First, find the side length (s):

**r = 9 inches**
**sin(π/5)** (or sin(36°)) is approximately **0.58778**
**s = 2 × r × sin(π/5)**
**s = 2 × 9 inches × 0.58778**
**s = 18 inches × 0.58778**
**s ≈ 10.58004 inches**

Now that we have 's', we can find the area using the formula Area = (5 × s²) / (4 × tan(π/5)):

**s² = (10.58004 inches)² ≈ 111.9372 inches²**
**tan(π/5)** (or tan(36°)) is approximately **0.72654**
**5 × s² = 5 × 111.9372 = 559.686**
**4 × tan(π/5) = 4 × 0.72654 = 2.90616**
**Area = 559.686 / 2.90616 ≈ 192.585 inches²**

Rounding to two digits

Area of a Pentagon

How to Find the Area of a Pentagon in 3 Easy Steps — Mashup Math

Pentagon Shape - Definition, Properties, Formulas, Examples

Pigimail Entertainment

Unlocking The Area Of A Pentagon: Your Guide To Calculating This Unique Shape

Table of Contents