What Is A Constant In Math? Unpacking Fixed Values In Equations
Have you ever looked at a math problem and wondered what makes some numbers hold their ground while others seem to change their identity? Well, that's where the idea of a constant comes into play, you know. It’s a pretty fundamental concept that brings a lot of order to the world of numbers and symbols. Understanding what a constant is can really make a difference in how you approach everything from basic algebra to more complex scientific formulas, actually.
According to my text, a constant is simply a fixed value that doesn't budge in a mathematical expression or equation, so it's always the same. Think of it like a steady anchor in a sea of changing numbers. These unchanging values show up everywhere, helping us build formulas that work consistently and giving us a solid base for calculations. Knowing how to spot these steady numbers is, in some respects, a key skill for anyone learning math.
This article will take a closer look at what constants are, how they differ from other parts of an equation, and why they matter so much. We’ll explore examples from algebra, geometry, and even physics, helping you get a good handle on these important mathematical building blocks. By the time we’re done, you’ll have a clear picture of these steadfast numbers and symbols, and how they provide stability in our mathematical journey, you know.
- Who Do You Think You Are I Am
- Married At First Sight Season 18
- Where Did Steve Horstmeyer Go To High School
- What Is The Healthiest Energy Drink
- How To Measure Inseam
Table of Contents
- What Exactly is a Constant?
- Constants vs. Variables: A Clear Difference
- Constant Terms in Algebraic Expressions
- Beyond Basic Numbers: Mathematical and Physical Constants
- Why Constants are so Important
- Frequently Asked Questions (FAQs)
What Exactly is a Constant?
The Core Idea
At its heart, a constant is a value that just doesn't change, according to my text. It's a fixed number, a symbol, or even a quantity that keeps its meaning and value throughout a math problem or expression. Think of it as something that remains the same, no matter what else is happening around it in the equation. This unchanging nature is, you know, what makes it so useful in math.
My text tells us that in an algebraic expression, a constant term is a part that doesn't have any variables attached to it and always has a set value. It's just a number that stands by itself. For instance, in the expression 3x + 7, that "7" is the constant. It doesn't have an 'x' or 'y' with it, so its value stays fixed, pretty much always.
This idea of something "unchanging" is, actually, a big part of what the word "constant" means in mathematics. It's a fixed numerical value that doesn't change in any situation, offering a steady point of reference. Whether it's a simple number like 5 in "x + 5," or a more complex symbol, its job is to provide that stability, you know.
- Thank You In Spanish
- Best Remoteiot Vpc
- High Potential Season 2
- Salvage Hunters Tee
- Ripple Ceo Brad Garlinghouse Xrp Tattoo
Constants in Different Math Areas
Constants aren't just for algebra; they pop up in lots of different math topics, my text explains. You'll find them in geometry, where they might represent a specific measurement that doesn't alter, or in physics, where they can describe fundamental properties of the universe. They're like the reliable friends you can count on in any mathematical setting, you know.
For example, in geometry, if you're working with the dimensions of a specific shape, a side length that's given as "10 units" would be a constant for that particular problem. It won't suddenly become "12 units" halfway through your calculations. This fixed nature helps us, in some respects, build accurate models and solve problems precisely.
My text also mentions that the word "constant" can have multiple meanings, but they all circle back to this idea of being "unchanging with respect to some other value." Whether it's a simple number in an expression or a deeper mathematical concept, its core role is to stay put. This consistency is, frankly, what gives math its reliable structure, right?
Constants vs. Variables: A Clear Difference
Understanding Variables
To really get what a constant is, it helps to see what it isn't. The opposite of a constant is a variable, according to my text. While a constant stays the same, a variable is something that can change or take on different values. Variables are usually represented by letters, like 'x' or 'y', and their values aren't fixed; they can vary depending on the situation or problem, you know.
Imagine you're trying to figure out how much money you'll earn if you work different numbers of hours. Your hourly wage might be a constant, say $15 per hour. But the number of hours you work, that's a variable. It could be 5 hours, 10 hours, or 20 hours. That's a classic example of how variables, actually, bring flexibility to equations.
So, a variable is subject to change and can take on different values or forms, my text explains. This means that unlike a constant, you can't always point to a variable and say "its value is definitively this number" without more information. They're the parts of an equation that we often try to solve for, or that represent quantities that can shift, you know.
Spotting the Difference
Spotting the difference between constants and variables is pretty straightforward once you get the hang of it. My text points out that a constant is a number on its own, without any variables attached. If you see a number like 7, or 12, or even a symbol like π (pi), standing alone or as part of a term without a letter next to it, it's very likely a constant, you know.
On the other hand, if you see a letter like 'x', 'y', 'a', or 'b' in an expression, that's generally a variable. If a number is directly next to a letter, like in "3x," the 'x' is the variable, and the '3' is what we call a coefficient, which is a constant multiplied by a variable. But the '3' itself, if it were standing alone, would be a constant, you know.
My text makes it clear: while variables like x or y can change or take on different values, a constant never changes—it's fixed. This distinction is, in some respects, one of the most basic and important things to learn in math. It helps us understand the structure of equations and how different parts behave, so it's really useful.
Constant Terms in Algebraic Expressions
Identifying Them
In algebra, we often talk about "constant terms" within expressions. My text defines a constant term as a term that doesn't contain any variables and has a fixed value. It's simply a number that stands alone in the expression. This makes them fairly easy to pick out once you know what you're looking for, you know.
Let's take an expression like 5x² + 2x - 8. In this example, the "5x²" has a variable (x), and so does "2x." But that "-8" at the end? That's a constant term. It's just a number, not tied to any changing variable, so it keeps its value no matter what 'x' might be. It's, basically, a standalone number.
My text gives another clear example: in the expression x + 5, the 5 is the constant. It's a number that doesn't have a letter next to it, so its value is set. Learning how to identify these terms is, actually, a foundational step in algebra, helping you break down and understand more complex equations.
Why They Matter
Constant terms are, in some respects, the backbone of algebraic expressions. They provide a fixed part of the value, which is incredibly useful when you're trying to solve for variables or understand the overall behavior of an expression. Without them, expressions would be a lot less stable and predictable, you know.
When you're working with equations, constants often represent an initial amount, a baseline, or a fixed cost. For example, if you're calculating the cost of a taxi ride, there might be a constant initial fee (the constant term) plus a per-mile charge (which involves a variable). The fixed fee is, really, always there, regardless of distance.
My text says that constants provide stability and consistency in mathematics. They allow us to create formulas that work in many situations, helping us understand relationships between quantities. A constant term, specifically, gives a stable point within an algebraic expression, which is pretty important for accurate calculations, you know.
Beyond Basic Numbers: Mathematical and Physical Constants
Famous Math Constants
While we often think of constants as simple numbers like 7 or 5, the idea goes much deeper. My text mentions "mathematical constants" and "physical constants" as terms sometimes used to distinguish broader meanings. These are key numbers whose value is fixed by a very clear definition, and they show up across all kinds of advanced math and science, you know.
One of the most famous mathematical constants is π (pi), which is approximately 3.14159. My text refers to π as a mathematical constant when discussing the volume of a sphere or the arclength of a circle. Its value is always the same, no matter what circle you're measuring. This unchanging nature is, actually, what makes it so universally useful.
Another well-known mathematical constant is 'e' (Euler's number), which is about 2.71828. These constants aren't just arbitrary numbers; they emerge from fundamental mathematical relationships and are crucial for calculations in calculus, geometry, and many other areas. They are, in a way, fixed truths of the mathematical world, you know.
Constants in the Real World
Constants aren't just abstract ideas; they have real-world applications, especially as physical constants. My text notes that a constant is essential in mathematics, physics, and chemistry for providing stability and predictability in equations and models. These are values that describe fundamental properties of our universe that don't change, you know.
Think about the speed of light in a vacuum, often denoted as 'c'. This is a physical constant, approximately 299,792,458 meters per second. No matter where or when you measure it, its value stays the same. Similarly, the gravitational constant 'G' is a fixed value that helps us calculate the force of gravity between any two objects. These are, basically, the unchanging rules of the universe.
My text even mentions finding an approximate value for a "constant of proportionality, k, in the solar system," which highlights how constants help us understand and model the physical world around us. These constants allow scientists and engineers to create formulas that accurately predict outcomes and design technologies that work reliably, so they're pretty important.
Why Constants are so Important
Building Stable Formulas
Constants are truly vital because they bring stability and consistency to mathematics, my text says. They are the fixed points that allow us to build formulas that work reliably, time after time. Imagine trying to calculate anything if all the numbers were constantly shifting; it would be a bit of a mess, you know.
Because constants hold their value, they let us create mathematical models that are predictable. Whether it's a simple formula for calculating area or a complex equation describing a chemical reaction, the constants within those formulas ensure that the results are consistent every time you apply them. This makes math a powerful tool for understanding our world, you know.
My text emphasizes that constants provide stability and consistency, helping us understand relationships between quantities. They give us fixed points from which to measure and compare. This foundational role means that constants are, actually, indispensable for any kind of serious mathematical work, from school homework to cutting-edge research.
Solving Problems Accurately
Constants are absolutely essential for solving problems accurately, my text states. Because their values are known and don't change, they provide a solid foundation for calculations. When you're trying to find an unknown variable in an equation, having those constant values locked in makes the process much more manageable and reliable, you know.
For example, if you're using a formula to calculate the volume of a cylinder, you'll need the constant π, and probably a fixed radius or height for a specific problem. Knowing that π is always approximately 3.14159 means you can trust that part of your calculation. This fixedness helps prevent errors and ensures your answers are correct, which is pretty important.
As of November 20, 2023, understanding these fixed values is more vital than ever, especially with so much information available. Constants provide stability and predictability in equations and models, according to my text. They are the unchanging anchors that help us navigate the sometimes tricky waters of mathematical problem-solving. To learn more about constants on our site, you can find many helpful resources, you know.
So, the next time you see a number standing alone in an equation, remember it's probably a constant, doing its important job of keeping things steady. These fixed values are fundamental to how math works, helping us create accurate formulas and solve problems with confidence. Keep exploring and you'll see just how much these unchanging numbers contribute to everything, you know. To explore other math basics, feel free to browse our collection of articles.
Frequently Asked Questions (FAQs)
What is an example of a constant in math?
A very common example of a constant in math is the number 7 in the expression 3x + 7, you know. The number 7 stands alone and doesn't have any variables attached, so its value is fixed and won't change. Another good example is the number 5 in the expression x + 5, which is, basically, always just 5.
What is the difference between a constant and a variable?
The main difference is that a constant is a fixed value that does not change, while a variable is a value that can change or take on different forms, my text explains. Constants are usually just numbers, like 10 or π, but variables are typically represented by letters, such as 'x' or 'y', and their value can shift depending on the problem, you know.
Why are constants important in math?
Constants are really important because they provide stability and consistency in mathematics, according to my text. They allow us to create formulas that work in many different situations and help us understand relationships between quantities. They give us fixed points that are essential for solving problems accurately and making predictions, so they're pretty foundational, you know.
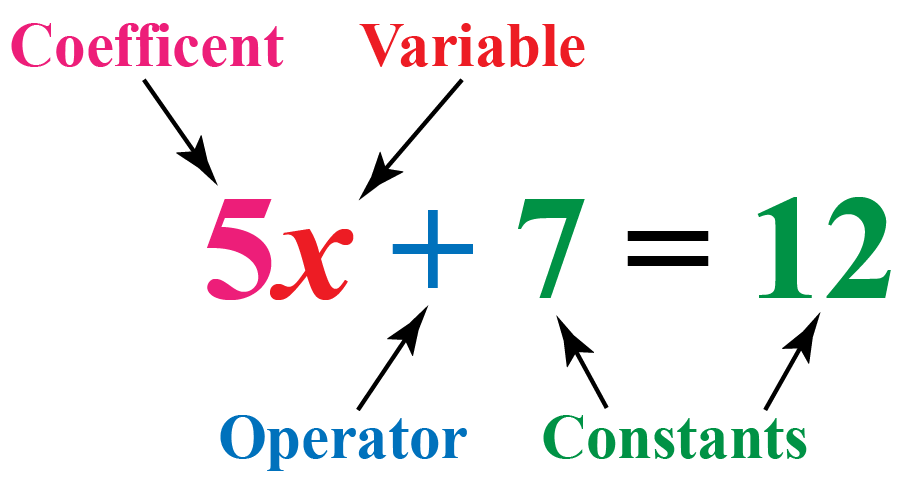
Discover what a constant means in math - Cuemath

Constant Definition (Illustrated Mathematics Dictionary)

What is a Constant | Definition of Constant